MECÂNICA GRACELI - QUÂNTICA TENSORIAL DE CAMPOS [600]

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

[

$\psi ^{*}$

$TeoriaInteraçãomediadorMagnitude relativaComportamentoFaixaCromodinâmicaForça nuclear forteGlúon10411/r71,4 × 10-15 mEletrodinâmicaForça eletromagnéticaFóton10391/r2infinitoFlavordinâmicaForça nuclear fracaBósons W e Z10291/r5 até 1/r710-18 mGeometrodinâmicaForça gravitacionalgráviton101/r2infinito$

Teoria	Interação	mediador	Magnitude relativa	Comportamento	Faixa
Cromodinâmica	Força nuclear forte	Glúon	1041	1/r7	1,4 × 10-15 m
Eletrodinâmica	Força eletromagnética	Fóton	1039	1/r2	infinito
Flavordinâmica	Força nuclear fraca	Bósons W e Z	1029	1/r5 até 1/r7	10-18 m
Geometrodinâmica	Força gravitacional	gráviton	10	1/r2	infinito

Em teoria quântica de campo, a função de correlação de n pontos é definida como a média funcional (valor esperado funcional) de um produto de $�$ operadores de campo em posições diferentes

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

C_{n}\left(x_{1},x_{2},\ldots ,x_{n}\right):=\left\langle \phi (x_{1})\phi (x_{2})\cdots \phi (x_{n})\right\rangle ={\frac {\int {\mathcal {D}}\phi \;e^{-S[\phi ]}\phi (x_{1})\cdots \phi (x_{n})}{\int {\mathcal {D}}\phi \;e^{-S[\phi ]}}}

Para funções de correlação dependentes do tempo, é necessário incluir o operador de ordenação temporal, $�$ .

O termo função de Green é certas vezes generalizado para descrever qualquer função de correlação de n pontos, em vez de apenas funções de dois pontos.

A função de correlação de dois pontos pode ser interpretada fisicamente como a amplitude de propagação de uma partícula ou excitação entre dois pontos no espaço-tempo. Na teoria livre, esta corresponde simplesmente ao propagador de Feynman.^[1]

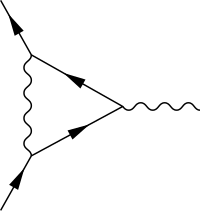
Na eletrodinâmica quântica, a função de vértice descreve o acoplamento entre um fóton e um elétron além da ordem principal da teoria das perturbações.^[1]^[2] Em particular, é a função de correlação irredutível de uma partícula envolvendo o férmion $\psi$ , o antifermion ${\bar {\psi }}$ e o potencial vetorial A.^[3]^[4]

Definição

A correção de um loop para a função de vértice. Esta é a contribuição dominante para o momento magnético anômalo do elétron.

A função de vértice $\Gamma ^{\mu }$ pode ser definida em termos de uma derivada funcional^[5] da ação efetiva S_eff as

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\Gamma ^{\mu }=-{1 \over e}{\delta ^{3}S_{\mathrm {eff} } \over \delta {\bar {\psi }}\delta \psi \delta A_{\mu }}

A contribuição dominante (e clássica) para $\Gamma ^{\mu }$ é a matriz gama $\gamma ^{\mu }$ , o que explica a escolha da letra. A função de vértice é restringida pelas simetrias da eletrodinâmica quântica — Invariância de Lorentz; invariância de calibre ou transversalidade do fóton, conforme expresso pela identidade de Ward; e invariância sob paridade - para assumir a seguinte forma:

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\Gamma ^{\mu }=\gamma ^{\mu }F_{1}(q^{2})+{\frac {i\sigma ^{\mu \nu }q_{\nu }}{2m}}F_{2}(q^{2})

onde $\sigma ^{\mu \nu }=(i/2)[\gamma ^{\mu },\gamma ^{\nu }]$ , $q_{\nu }$ é o quadrimomento de entrada do fóton externo (no lado direito da figura), e F₁(q²) e F₂(q²) são fatores de forma^[6] que dependem apenas da transferência de momento q². No nível da árvore (ou ordem inicial), F₁(q²) = 1 e F₂(q²) = 0. Além da ordem inicial, as correções para F₁(0) são exatamente cancelados pela renormalização da intensidade do campo.^[7]^[8] O fator de forma F₂(0) corresponde ao momento magnético anômalo^[9]^[10] a do férmion, definido em termos do fator g de Landé^[11]^[12] como:

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

a={\frac {g-2}{2}}=F_{2}(0)

Na física teórica, especificamente na teoria quântica de campos, uma função beta, β(g), codifica a dependência de um parâmetro de acoplamento, g, na escala de energia, μ, de um determinado processo físico descrito pela teoria quântica de campos.^[1] É definido como

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\beta (g)={\frac {\partial g}{\partial \log(\mu )}}~,

^[2]

e, por causa do grupo de renormalização subjacente, ele não tem dependência explícita de μ, portanto, depende apenas de μ implicitamente por meio de g. Essa dependência da escala de energia assim especificada é conhecida como a execução do parâmetro de acoplamento, uma característica fundamental da dependência de escala na teoria quântica de campos, e sua computação explícita pode ser alcançada por meio de uma variedade de técnicas matemáticas.^[3]

A formulação de Feynman da mecânica quântica ou formulação de integrais de caminho da mecânica quântica é uma descrição da teoria quântica que generaliza a ação da mecânica clássica. Ela substitui a noção clássica de uma única trajetória para um sistema por uma soma, ou integral funcional, por meio de uma infinidade de trajetórias possíveis para calcular a amplitude quântica.

A ideia básica da formulação de integral de caminho é originária de Norbert Wiener, que apresentou o processo de Wiener para a solucionar problemas de difusão e movimento Browniano.^[1] Esta ideia foi estendida para o uso do Lagrangiana na mecânica quântica por P. A. M. Dirac em seu artigo de 1933^[2] . O método completo foi desenvolvido em 1948 por Richard Feynman. Algumas preliminares foram trabalhados anteriormente, no curso de sua tese de doutorado no trabalho de John Archibald Wheeler. A motivação original surgiu da aspiração de obter uma formulação da mecânica quântica para a teoria de teoria de ação à distância de Wheeler e Feynman usando uma Lagrangeana (ao invés de um Hamiltoniano) como ponto de partida.

Esta formulação tem se provado fundamental para o desenvolvimento posterior da física teórica, por ser manifestamente simétrica entre o tempo e o espaço. Ao contrário dos métodos anteriores, a formulação de integral de caminho-integral permite facilmente a mudança de coordenadas entre descrições canônicas diferentes do mesmo sistema quântico.

A formulação de integral de caminho também relaciona processos quânticos e estocásticos, fornecendo a base para a grande síntese, na década de 1970 que unificou a teoria quântica de campos com a teoria de campos estatísticos de campo flutuante perto de uma transição de fase de segunda ordem. A equação de Schrödinger é uma equação de difusão com uma constante de difusão imaginária, sendo a integral de caminho uma continuação analítica do método para a soma de todos as possíveis caminhadas aleatórias. Por esta razão integrais de caminho foram utilizados no estudo de difusão e movimento Browniano pouco antes de serem introduzidos na mecânica quântica.^[3]

Estes são apenas três dos caminhos que contribuem para amplitude quântica de uma partícula movendo-se do ponto A em tempo t₀ para o ponto B em t₁.

Princípio da ação quântica

Na mecânica quântica, assim como na mecânica clássica, o Hamiltoniano é o gerador de translações temporais. Isto significa que o estado em um tempo posterior difere do estado atual pela atuação do operador Hamiltoniano (multiplicado pelo negativo unidade imaginária, −i). Para os estados com uma determinada energia, esta é uma instrução de relação de De Broglie entre a frequência e a energia, e a relação geral é consistente com o que e o princípio da superposição.

No entanto, na mecânica clássica o Hamiltoniano é derivado a partir de um Lagrangeana, que é uma quantidade mais fundamental em relação à relatividade especial. O Hamiltoniano indica como o movimento se desenvolve no tempo, mas o tempo é diferente em diferentes sistemas de referência. Assim, o Hamiltoniano é diferente em referenciais diferentes e este tipo de simetria não é aparente na formulação original da mecânica quântica.

O hamiltoniano é uma função da posição e momento no tempo t, determinando a posição e o momento no tempo (t+ε). A Lagrangiana é uma função das posição em t e (t+ε) (para um intervalo de tempo infinitesimal, a velocidade é medida é a velocidade instantânea, tornando a Lagrangeana como função da posição e da velocidade). A relação entre os dois é por uma transformação de Legendre e a condição que determina as equações de movimento (ou equações de Euler–Lagrange) é a extremização da ação.

Na mecânica quântica, uma transformação de Legendre é difícil de interpretar uma vez que o movimento não é dado por uma trajetória definida. Na mecânica clássica, a discretização temporal da transformação de Legendre torna-se:

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\epsilon H=p(t)(q(t+\epsilon )-q(t))-\epsilon L\,

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

p={\partial L \over \partial {\dot {q}}}\,

onde a derivada parcial com relação a mantém q(t + ε) constante. A inversa da transformação de Legendre é:

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\epsilon L=\epsilon p{\dot {q}}-\epsilon H\,

onde

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\dot {q}}={\partial H \over \partial p}\,

tomando q fixo.

Na mecânica quântica, um estado qualquer é uma superposição de estados independentes, com diferentes valores de q, ou diferentes valores de p, sendo que o momento e a posição (p e q) podem ser interpretadas como operadores que não comutam. O operador p é definitivo em estados onde q são indeterminados. Considere dois estados separados no tempo. A atuação do operador correspondente à Lagrangiana:

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

e^{i(p(q(t+\epsilon )-q(t))-\epsilon H(p,q))}\,

Se a multiplicação implícita na fórmula são reinterpretados como multiplicação de matrizes, o primeiro fator é:

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

e^{-ipq(t)}\,

Se esse também é interpretado como uma multiplicação de matrizes, a soma sobre todos os estados integra todos q(t), levando a transformada de Fourier em q(t), mudando a base para p(t). Isto é a ação sobre o espaço de Hilbert – mudar de base para p no tempo t.

Em seguida, tem-se:

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

e^{-i\epsilon H(p,q)}\,

que é uma evolução infinitesimal para o futuro.

Finalmente, o último fator, nessa interpretação, é:

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

e^{ipq(t+\epsilon )}\,

que é uma mudança de base de volta para q no tempo (t+ε).

Isto não é diferente do operador de evolução temporal: o fator H contém toda informação da dinâmica, avançando o estado no tempo. A primeira e a última parte são as transformadas de Fourier para a mudança na base pura de q a partir de uma base intermediária p.

De forma equivalente, pode-se dizer que: uma vez que o Hamiltoniano é naturalmente uma função de p e q, exponenciando estas quantidades e realizando uma mudança de base de p para q em cada passo permite expressar o elemento da matriz de H como uma função simples ao longo de cada caminho. Esta função é o análogo quântico da ação clássica. Esta observação é feita por Paul Dirac.

Dirac observou ainda que se pudesse, o quadrado do tempo-a evolução do operador no S representação:

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

e^{i\epsilon S}\,

e isso é o operador de evolução temporal entre o tempo t e o tempo t + 2ε. Enquanto que na representação H a quantidade que está sendo somada nos estados intermediários é um elemento de matriz obscuro, na representação S esta é reinterpretado como uma quantidade associada ao caminho. No limite que leva um grande poder de esse operador, reconstrói-se a evolução quântica completa entre dois estados sendo o estada mais antigo com valor fixo q(0) a o estado mais recente com valor q(t). O resultado é uma soma sobre os caminhos com uma fase que é a ação quântica. Crucialmente, Dirac identificada neste papel, a profundidade da mecânica quântica razão do princípio da mínima ação de controlar o limite clássico.

Interpretação de Feynman

O trabalho de Dirac não fornece uma prescrição para calcular a soma sobre os caminhos e não mostra como recuperar a equação de Schrödinger ou as relações de comutação canônica a partir desta regra. Isto foi feito por Feynman^[4] , que sugeriu que no limite clássico a trajetória clássica surge naturalmente.

Feynman mostrou que a ação quântica de Dirac foi, para a maioria dos casos de interesse, simplesmente igual a ação clássico, devidamente discretizado. Isso significa que a ação clássica é a fase adquirida pela evolução quântica entre dois pontos fixos. Feynman propõe a recuperação de toda a mecânica quântica a partir dos seguintes postulados:

A probabilidade de um dado evento é dado pelo modulo quadrado de uma quantidade chamada de "amplitude de probabilidade".
A amplitude de probabilidade é dado somando a contribuição de todos os caminhos no espaço de configurações
A contribuição de um caminho em particular é proporcional à $e^{iS/\hbar }$ , onde S é a ação dado pela integral temporal da Lagrangeana ao longo do caminho.

Para encontrar a amplitude de probabilidade global para um determinado processo, soma-se, ou integra-se, a amplitude do 3º postulado sobre o espaço de todos os possíveis caminhos de sistema entre o estado inicial e o estado final, inclusive aqueles que são absurdos para o caso clássico. No cálculo da amplitude de probabilidade para uma única partícula, indo de uma coordenada espaço-tempo de coordenadas para outro, é correto incluir caminhos em que a partícula descreve trajetórias elaboradas,(curlicues) curvas em que a partícula dispara para o espaço sideral e volta novamente, e assim por diante. A integral de caminho integral atribui a todas estas amplitudes um mesmo peso, variando a fase de cada um, ou o argumento do número complexo. Contribuições de caminhos muito diferentes da trajetória clássica pode ser suprimida por interferência (ver abaixo).

Feynman mostrou que esta formulação da mecânica quântica é equivalente a aproximação canônica da mecânica quântica quando o Hamiltoniano possui, no máximo, termos quadráticos no momento. Uma amplitude calculada de acordo com o princípio de Feynman irá também obedecer a equação de Schrödinger para o Hamiltoniano correspondente à determinada ação.

A formulação de integral de caminho da teoria quântica de campos representa a amplitude de transição (correspondente a função correlação clássica) como uma soma ponderada de todos os possíveis histórias do sistema, de um estado inicial a um estado final. Um diagrama de Feynman é uma representação gráfica de uma contribuição perturbativa para a amplitude de transição.

Formulação concreta

Os postulados de Feynman são interpretados da seguinte maneira:

Definição da fração temporal (time-slicing)

Para uma partícula em um potencial suave, a integral de caminho é aproximada por caminhos em zig-zag, que, em uma dimensão, a integral de caminho é o produto de integrais ordinárias. Para o movimento de uma partícula que parte da posição x_ano tempo t_a e chega em x_b no tempo t_b, a sequência de tempo:

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

t_{a}=t_{0}<t_{1}<...<t_{n-1}<t_{n}<t_{n+1}=t_{b}

é dividida em (n + 1) segmentos de tempo (t_j − t_{j − 1)}, onde j = 1,...,n + 1, onde

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\epsilon =\Delta t={\tfrac {t_{b}-t_{a}}{n+1}}\,.

é uma duração de tempo fixo. Este processo é chamado de fração temporal (time-slicing).

Uma aproximação para a integral de caminho pode ser calculada como proporcional à

$equação Graceli estatística tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\int \limits _{-\infty }^{+\infty }\,\ldots \int \limits _{-\infty }^{+\infty }\,\ \exp \left({\frac {\rm {i}}{\hbar }}\int \limits _{t_{a}}^{t_{b}}L(x(t),v(t),t)\,\mathrm {d} t\right)dx_{0}\,\ldots \,dx_{n}

onde é a Lagrangiana do sistema unidimensional com posição x(t), velocidade v = ẋ(t) e dx_j corresponde à posição no j-ésimo passo de tempo, quando a integral temporal é aproximada por uma soma de n termos.^{[note 1]}

Pesquisar este blog

MECÂNICA GRACELI - QUÂNTICA TENSORIAL DE CAMPOS [600]

Definição

Princípio da ação quântica

Interpretação de Feynman

Formulação concreta

Definição da fração temporal (time-slicing)

Comentários

Postar um comentário

Postagens mais visitadas deste blog